The Relational Model, Part 2

Normalization and Data Design

This is part 2 of my series on the relational model. Part 1 can be found here (only for paid newsletter subscribers).

In this draft, I explore normalization, starting with some ground rules for normalization and then moving toward a working example of going from the first normal form to the Boyce-Codd normal form.

I’m making this article free for everyone, mainly because I sense that the relational model and normalization are dying arts. A working knowledge of the relational model will save you a lot of time and headaches, especially if you work with tabular data.

The topic of relational modeling is VAST, and this article/chapter will serve enough for you to get started. However, I suggest going further. Start with C.J. Date, who’s written many books (and thousands of pages) about relational modeling over the decades.

Here are some of Date’s books you should check out:

• SQL and Relational Theory

• Database Design and Relational Theory: Normal Forms and All That Jazz

• Fifty Years of Relational, and Other Database Writings

This draft will continue to be revised as I encounter any errors or additions that need to be made. Your constructive comments are much appreciated¹.

I’m also creating a course on data modeling based on this upcoming book. Stay tuned for video tutorials and other resources to help you learn data modeling via different mediums.

Thanks for your interest in data modeling,

Joe Reis

---

“Interviewer: Where did “normalization” come from?

Codd: It seemed to me essential that some discipline be introduced into database design. I called it normalization because then President Nixon was talking a lot about normalizing relations with China. I figured that if he could normalize relations, so could I.”²

So far, we've explored how data is structured in relations and how we can manipulate it. The discussions have been mostly theoretical, and you're probably wondering how to put these relational ideas into practice. Now, let's look at how to design these relations properly. Normalization is a systematic way to ensure relations are well-structured and free from certain data anomalies. In this section, we'll first learn some ground rules for normalization and then see how our e-commerce example evolves through different normal forms.

Ground Rules of Normalization

Numerous books and online resources cover normalization, but most skip to the mechanics without explaining why they are needed. Before diving into an example, let's look at how normalization solves data problems like dependencies, unintended side effects, etc.

Dependencies

A dependency is fundamentally about relationships between pieces of data - specifically, how one piece of data determines or requires another. Dependencies are often denoted as X -> Y, where X is a set of attributes that might determine the value of Y. Think of it as "if you know X, you can know Y." The attribute X is called the determinant, and Y is the dependent. If you remember from algebra, this is conceptually similar, where X is the independent variable, and Y is the dependent variable.

Let's look at a few simple, real-world examples:

• If you know someone's email address, you can determine their email domain (i.e., joe420@aol.com → aol.com).

• If you know a U.S. zip code, you can determine the city and state (e.g., 84101 → Salt Lake City, Utah).

• If you have a book's ISBN, you can determine its publisher (Fundamentals of Data Engineering ISBN 978-1098108304 → publisher = O’Reilly Media).

Let’s examine some of the dependencies you’ll need when normalizing data. This isn’t a complete list, but it will give you an idea of what dependencies are and how they’re used.

Functional Dependencies

In our e-commerce example, ProductID determines ProductName because each ProductID is associated with exactly one ProductName. So, if you know the ProductID, you know the ProductName. Unless the ProductName explicitly changes, say from “SmartPhone” to “SmarterPhone,” P001 will always refer to “SmartPhone.”

This is an example of a functional dependency, a relationship between two attributes in a relation, where one attribute's value determines the other's value. In other words, if you know the value of one attribute, you can indirectly determine the value of the other.

Let’s take a moment to explain a type of dependency you’ll encounter in the normalization examples later in the chapter: the non-trivial dependency. A non-trivial dependency is a relationship between two or more attributes in a relation, where the dependent attribute is strictly not a subset of the determinant. In other words, a non-trivial dependency occurs if X → Y, and Y is not a subset of X.

You might be wondering about the opposite case, a trivial dependency. In this case, the exact opposite occurs. Here, the dependent is always a subset of the determinant. If X → Y and Y is a subset of X, then it is a trivial dependency.

Let’s next look at a related (no pun intended) dependency.

Transitive Dependencies

You’re interested in some manufacturing information about a product. Consider this table, where we have a ProductID P001, a smartphone manufactured by Mega Tech Corp based in the USA. If you were only given the Manufacturer’s country, could you concretely determine the ProductID or the Manufacturer’s name? Now flip the question around. If given the ProductID, you would have the Manufacturer’s name (assuming that is the only manufacturer for that product). Given the Manufacturer’s name, your records show that Mega Tech Corp is based in the USA.

This is an example of a transitive dependency, where the value of an attribute in a relation determines the value of another attribute in the same relation, which determines the value of a third attribute. In other words, if attribute A determines attribute B and attribute B determines attribute C, attribute A transitively determines attribute C. This means that if you know the value of attribute A, you can indirectly determine the value of attribute C through attribute B.

A → B → C means A → C

While there are other dependencies like join and multivalued dependencies, functional and transitive dependencies are sufficient for most relational modeling you’ll do.

The goal of identifying dependencies is to remove or minimize them. Let’s next examine some of the anomalies these dependencies can cause.

Anomalies, aka Side Effects

The side effects of dependencies are painfully pervasive. If you’ve dealt with data anywhere in the data lifecycle, I’m sure you’ll attest that data’s often a mess. Dependencies in your dataset increase the risks of anomalies, especially if you need to change your data in multiple places. How do you make changes to this data? As you probably know, this is extremely painful and tedious. Thankfully, as you’ll find out, it’s also preventable.

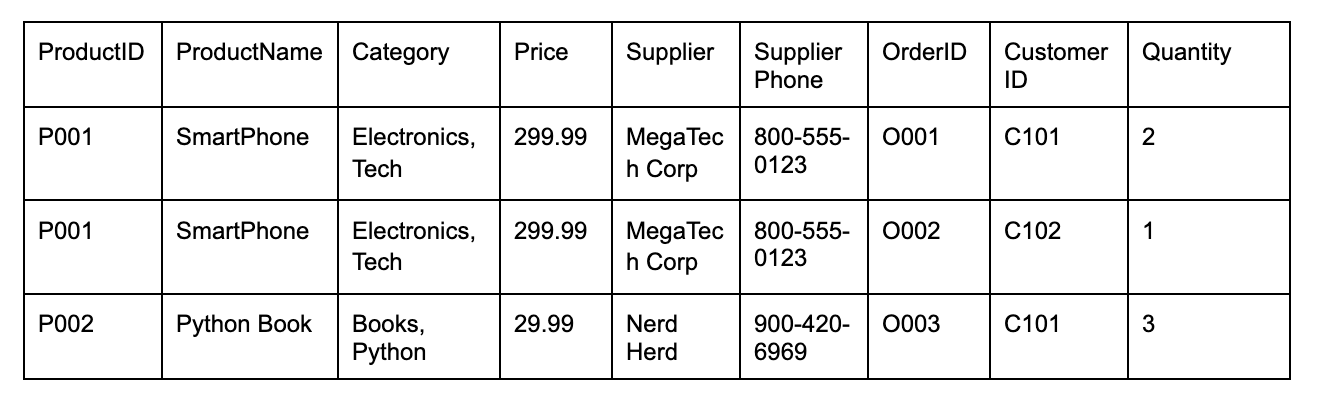
Data can be inserted (created), updated, and deleted. These are all opportunities for problems if the data isn’t well modeled. Imagine you have a single table for Products and Orders, like the one below, if you want to add a new product record to this table. An insertion anomaly occurs because you cannot do so without adding information about the order (OrderID, CustomerID, Quantity, etc). The product information is tied to everything else in the table.

Given this same table, if a product’s price changes, you must update every order record that includes that product. If you miss a record, you’ll have different prices for the same product. This is an example of an update anomaly.

Finally, let’s say a first-time customer bought a product from your site and discovered they were charged a higher price than what was listed on the site. They want to close their account and remove their data from your systems. Due to data privacy regulations, you must delete this customer’s information. You look into the problem and realize the problem isn’t just a single table like the one above. Multiple tables in your database have varying product information and prices. Oops…Now, you not only have to update the prices in these different tables, but you need to delete the customer’s record in the above table. You no longer have this information about the customer or what they ordered.

If this example seems familiar, rest assured you’re not alone. I’ve seen things like this (and worse) in organizations big and small and of varying levels of technical sophistication. It seems like nobody is immune to the consequences of data anomalies. Pay attention to dependencies and their impact on update anomalies. Nobody wants unintended side effects on their data, and many of these problems can be alleviated or eliminated with a bit of upfront thought and planning in your data modeling. These are the anomalies the relational model aims to prevent.

Normal Forms Are Hierarchical

So far, you’ve learned some rules for managing dependencies and their associated side effects. It’s now time to tie it together with normalization. In normalization, we seek to create progressively better normal forms of data that follow a set of rules and guidelines to minimize data redundancy and improve data integrity. Normal forms are hierarchical. It’s not common to jump straight to the highest normal form. What most often happens is we start from a base normal form and whittle away until we get something that’s a higher normal form. A relation might begin in the first Normal Form (1NF). Going forward, we’ll shorten “Normal Form” to NF for brevity.

Here’s the hierarchy of normal forms, starting with 1NF.

1NF - lowest level of normalization

2NF

3NF

Boyce Codd NF (BCNF)

4NF

5NF

6NF - very high normalization

Normalization is hierarchical from 1NF to BCNF because each successive normal form builds on the rules of the previous one, progressively addressing increasingly complex data anomalies and dependencies. So, a dataset in 2NF is implicitly 1NF, 3NF is also 2NF, and so on.

In the following example, we’ll explore moving from 1NF to BCNF; 4NF and higher are mentioned simply to indicate their existence.

An Example of Going from 1NF to BCNF

The normalization process normally (no pun intended) goes from a big dataset to many discrete datasets. In this exploration of the normalization process, we’ll go in this order.

Let's start with a single relation that tries to capture everything about products and orders.

PRODUCTS_AND_ORDERS

You saw this schema earlier. As you recall, it’s littered with all sorts of problems. Let's normalize this table to make it less crappy.

First Normal Form (1NF)

We’ll start with the First Normal Form (1NF), the first step toward normalizing our data. It requires that:

1. Each column contains atomic (indivisible) values.

2. Each column contains values from the same domain.

3. Each column has a unique name.

4. The order of rows and columns doesn't matter.

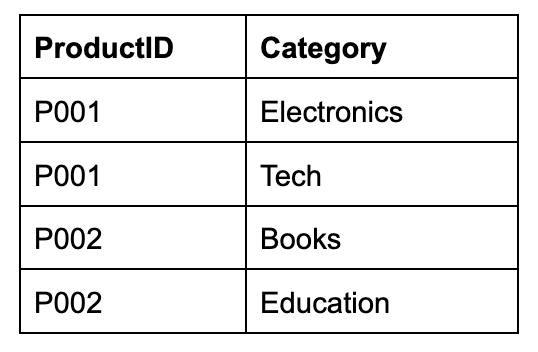
First, notice that the Category column allows multiple values (i.e., Electronics, Tech). For simplicity, let’s zoom in on this below with a table called BAD_PRODUCTS. The Category column violates the atomicity rule since each cell contains multiple pieces of information. This table would be called denormalized or unnormalized. We’ll get into the differences of each type of table later in the chapter.

BAD_PRODUCTS

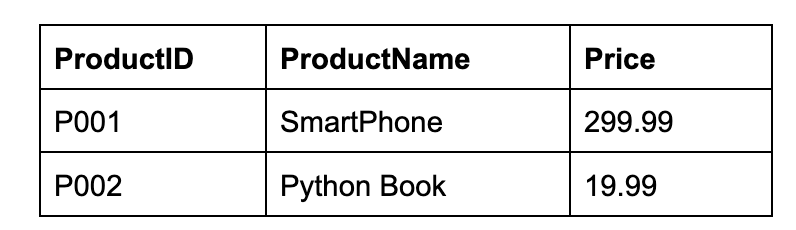
To make this 1NF compliant, we split the categories into a separate table, PRODUCT_CATEGORIES, with each Category mapped to a ProductID.

PRODUCTS

PRODUCT_CATEGORIES

This fixes the multi-valued cells in the Category column, and our data is now 1NF compliant. However, there’s still more work to do.

Second Normal Form (2NF)

The Second Normal Form (2NF) requires that the relation is in 1NF and that all non-key attributes are functionally dependent on the primary key.

Let’s go back to our PRODUCTS_AND_ORDERS table and its columns.

PRODUCTS_AND_ORDERS

Here, ProductName, Category, Price, Supplier, and SupplierPhone depend only on ProductID, not the entire key (ProductID, OrderID). Since we don’t need the other columns in this table, let’s split them into separate tables.

PRODUCTS

ORDERS

The PRODUCTS table contains information related to the ProductID, and the ORDERS table similarly has data about orders. In both cases, the information in each table is fully functionally dependent on the primary key for that table. But we’re not done. You might notice some transitive dependencies. Let’s tackle those.

Third Normal Form (3NF)

3NF requires that the relation is in 2NF, and no non-key attribute is transitively dependent on the primary key. Notice in PRODUCTS that SupplierPhone depends on Supplier, which depends on ProductID. Also, Category depends on the ProductID, and can be split into its own table.

Let's convert PRODUCTS from 2NF to 3NF by creating a new CATEGORIES and SUPPLIERS table and some additional information we’ll need for the following example.

PRODUCTS

CATEGORIES

ORDERS

SUPPLIERS

SUPPLIER_CAPABILITIES

Now, every table conforms to 3NF. But we can take it a step further and remove even more dependencies.

Boyce-Codd Normal Form (BCNF)

Finally, we arrive at the Boyce-Codd Normal Form (BCNF or 3.5NF). BCNF is a stricter version of 3NF, and it aims to eliminate non-trivial functional dependencies where the determinant is not a superkey. You might recall superkeys from our earlier discussion on identifiers, but as a reminder, a superkey is simply a combination of columns that can uniquely identify a row.

The core idea of BCNF is that each determinant must be a candidate key. If a functional dependency A -> B is in a table, then A should be a candidate key uniquely identifying a row. If a determinant is not a candidate key, you might have redundant data or trouble updating or deleting records. BCNF aims to eliminate redundancy and anomalies that can still occur even in 3NF. Let’s continue with our 3NF example above.

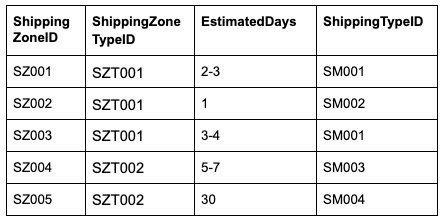
The SHIPPING_ZONES table has a lot we can work with. Let’s look at how we can improve on this table.

SUPPLIERS

SHIPPING_ZONES

SHIPPING_ZONE_TYPES

SHIPPING_METHODS

SUPPLIER_SHIPPING_CAPABILITIES

That's it! All our tables are now compliant with BCNF. While we can continue normalizing further with 4NF and beyond, this will be sufficient for most situations. In my experience, and with data modelers I've spoken with, normalization up to 3NF is often adequate. BCNF removes even more redundancies and anomalies. According to C.J. Date and others, BCNF is where data is truly fit for purpose. You can continue normalizing past BCNF, and I'll leave it to you to decide how far you want to go.

Lossless Composition and Decomposition

In the above BCNF example, the normalization process took a table and decomposed it into several smaller tables. This is known as the lossless property of the relational model (sometimes called the closure rule), where we must be able to reconstruct the original relation entirely through joins without losing or gaining information. If you can decompose the data in one direction, you should be able to recompose the data to its original form in the opposite direction. The lossless property assumes that keys and joins are unambiguous and properly related. Moving from one relational form to another helps maintain bi-directional data integrity in the relational model.

For example, when we moved from 3NF to BCNF, we decomposed the SUPPLIERS relation into several smaller relations. All of the functional dependencies from the original relation were preserved. Reversing this BCNF decomposition and recreating the original 3NF SUPPLIERS relation should be easily achievable without losing attributes.

Now that you understand normalization let’s finish this chapter with some considerations and thoughts about the relational model, especially as it stands today.

1. Updated 1/7/2024. Thanks to Donald Parish for pointing out some tweaks to be made in the 3NF and BCNF examples. I’ll continue refining these as needed.

2. A Fireside Chat: Interview with Dr. Edgar F. Codd (DBMS Magazine 6, No. 13, December 1993)